Приложение
Как установить приложение на iOS
Смотрите видео ниже, чтобы узнать, как установить наш сайт в качестве веб-приложения на домашнем экране.
Примечание: Эта возможность может быть недоступна в некоторых браузерах.
-
Уважаемый посетитель!!!
Если Вы уже являетесь зарегистрированным участником проекта "миХей.ру - дискусcионный клуб",
пожалуйста, восстановите свой пароль самостоятельно, либо свяжитесь с администратором через Телеграм.
Вы используете устаревший браузер. Этот и другие сайты могут отображаться в нём некорректно.
Вам необходимо обновить браузер или попробовать использовать другой.
Вам необходимо обновить браузер или попробовать использовать другой.
Высшая математика
- Автор темы Jennifer
- Дата начала
Если
Ассоциация критиков
В знаменателе получается корень пятой степени из t и натуральный логарифм от единицы деленной на t-1 - что это даст?Trotil написал(а):чем не подошла такая замена?
Trotil
Команда "У.М."
Если
По второму интегралу: http://www.reshebnik.ru/solutions/4/13/
твой случай (3)
Я правда не пробовал применить эту подстановку. Если запутаешься - скажи.
По второму интегралу: http://www.reshebnik.ru/solutions/4/13/
твой случай (3)
Я правда не пробовал применить эту подстановку. Если запутаешься - скажи.
Trotil
Команда "У.М."
Опишу кратко подстановку:
/x^2)
*(z^3+1)^(-1/2))
*(z^3+1)^(-3/2)*3*z^2*dz)
=3^(1/6)*{z^3+1}^(-1/6))
^(1/3)=z*x^(2/3)=z*3^(1/3)*(z^3+1)^(-1/3))
*(3-x^2)^(1/3)dx->3^(1/6)*{z^3+1}^(-1/6)*z*3^(1/3)*(z^3+1)^(-1/3)*\sqrt{3}*(-1/2)*(z^3+1)^(-3/2)*3*z^2*dz=(-1/2)*(z^3+1)^(-2)*z^3*3^(11/6))
Теперь надо решить^2*dz}=\int{(dz)/(z^3+1)}-\int{(dz)/(z^3+1)^2})
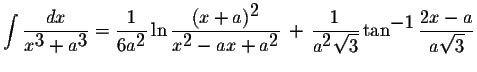
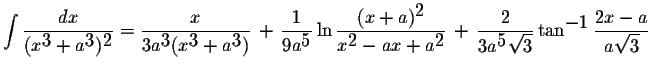
Брр... Должен быть какой путь проще, наверное. Мне кажется, когда, все это упростится, то окажется, что решением могла быть более простая подстановка... Хотя вряд ли.
Если
Ты учишься на редактора! Откуда там такие интегралы??? Это уровень технического вуза, не меньше.
Теперь надо решить
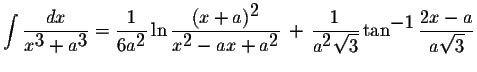
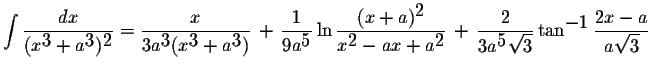
Брр... Должен быть какой путь проще, наверное. Мне кажется, когда, все это упростится, то окажется, что решением могла быть более простая подстановка... Хотя вряд ли.
Если
Ты учишься на редактора! Откуда там такие интегралы??? Это уровень технического вуза, не меньше.

Если
Ассоциация критиков
Trotil, спасибо.
Еще мой преподаватель сам попробует решить это чудо - посмотрю, может, у него будет проще.
Математика-информатика идет как неспециализированная дисциплина. На первом курсе такого много. А уровень работ, я думаю, задается нашим оптимистичным преподавателем с кафедры высшей математики, который на вопрос: "А зачем нам математика?" - отвечает: "Чтобы учить своих детей".
Но зато я теперь понимаю, что правильно не стала учиться на "Информационной безопасности", на которую поступила "на всякий случай". Это, конечно, все дико интересно, но таланта в этой области у меня точно нет. Хоть как-то разбираться мне помогают друзья, вспомогательные материалы и окончание политехнического класса - но ты же сам видишь, что я далеко, далеко, далек-о-о не Лейбниц .
.
Еще мой преподаватель сам попробует решить это чудо - посмотрю, может, у него будет проще.
Я учусь в уральском государственном техническом университете, бывшем политехе. Он и есть технический. Наша специальность - нет. Однако волей судьбы она живет на теплоэнергетическом факультете и является соседней по номеру с прикладной математикой.Trotil написал(а):Ты учишься на редактора! Откуда там такие интегралы??? Это уровень технического вуза, не меньше.
Математика-информатика идет как неспециализированная дисциплина. На первом курсе такого много. А уровень работ, я думаю, задается нашим оптимистичным преподавателем с кафедры высшей математики, который на вопрос: "А зачем нам математика?" - отвечает: "Чтобы учить своих детей".
Но зато я теперь понимаю, что правильно не стала учиться на "Информационной безопасности", на которую поступила "на всякий случай". Это, конечно, все дико интересно, но таланта в этой области у меня точно нет. Хоть как-то разбираться мне помогают друзья, вспомогательные материалы и окончание политехнического класса - но ты же сам видишь, что я далеко, далеко, далек-о-о не Лейбниц
 .
.Если
Ассоциация критиков
Мой преподаватель, попробовав это решить, сказал, что там явная опечатка и чтобы я его не решалаTrotil написал(а):Брр... Должен быть какой путь проще, наверное. Мне кажется, когда, все это упростится, то окажется, что решением могла быть более простая подстановка... Хотя вряд ли.
 .
.Извини за доставленные неудобства
 .
.Trotil
Команда "У.М."
Если

Но он решается Преподаватель не смог решить? А ты ему показывала решение мое?
Преподаватель не смог решить? А ты ему показывала решение мое?

Но он решается
 Преподаватель не смог решить? А ты ему показывала решение мое?
Преподаватель не смог решить? А ты ему показывала решение мое?Пустяки... Иногда полезно поломать голову )Если написал(а):Извини за доставленные неудобства
Если
Ассоциация критиков
Он, возможно, и смог, но решил меня не мучить, а настаивать я не сталаTrotil написал(а):Преподаватель не смог решить? А ты ему показывала решение мое?
 .
.Решение - нет, не показывала.
Trotil
Команда "У.М."
Если
http://www.mixei.ru/threads/57197
немного про информатику, но переносить не надо - вопрос вполне математический...
Табуляция функций - задача, выполняемая аналитически (для любого x можно подсчитать точное значение функции f(x))
Построение графиков - численная задача (аппроксимация кривых графика) - когда мы находим только ограниченное кол-во точек, а остальные точки графика получаем, соединяя точки ломаными и приближенными кривыми
С точки зрения информатики, машинных вычислительных процессов, первая задача тоже может рассматриваться, как численная, если мы заменяем полученные иррациональные числа (sin (30град), 7^(1/2) на десятичные дроби)
//что-то мне этот ответ не нравится... Надо переформулировать...//
http://www.mixei.ru/threads/57197
немного про информатику, но переносить не надо - вопрос вполне математический...
Аналитическое решение задачи подразумевает точное ее решение, нахождение точных ответов, численное - методы, позволяющие найти ответ с заданной точностью, когда аналитическое решение невозможно.В чем разница между численным и аналитическим методом?
Табуляция функций - задача, выполняемая аналитически (для любого x можно подсчитать точное значение функции f(x))
Построение графиков - численная задача (аппроксимация кривых графика) - когда мы находим только ограниченное кол-во точек, а остальные точки графика получаем, соединяя точки ломаными и приближенными кривыми
С точки зрения информатики, машинных вычислительных процессов, первая задача тоже может рассматриваться, как численная, если мы заменяем полученные иррациональные числа (sin (30град), 7^(1/2) на десятичные дроби)
//что-то мне этот ответ не нравится... Надо переформулировать...//
Последнее редактирование модератором:
Шедевра
Звезда
Не совсем стандартная просьба. Мне нужно не решить задачу, а получить консультацию по пространству функций  (видимо, это какое-то подпространство непрерывных функций). Буду признательна за любую информацию, ссылки и т.д. Просто встретилось в одной статье без дополнительных пояснений.
(видимо, это какое-то подпространство непрерывных функций). Буду признательна за любую информацию, ссылки и т.д. Просто встретилось в одной статье без дополнительных пояснений. 

Trotil
Команда "У.М."
Шедевра
А можно статью или контекст? Это что-то из функционального анализа наверное....
А можно статью или контекст? Это что-то из функционального анализа наверное....
Шедевра
Звезда
Trotil
Cама статья относится к области мат. физики и нелинейного анализа. Классические учебники (Колмогоров-Фомин, Владимиров и т.д.) ответа на мой вопрос не дали.
В самой статье написано так:
) принадлежит
принадлежит ) , а ее производная
, а ее производная  принадлежит
принадлежит )
inf - это бесконечность, я не знаю. как ее тут поставить
Короче, суть в том, что если есть функция одной переменной u(t) из) , а ее производная принадлежит
, а ее производная принадлежит ) , то мы получим ровно интересующее меня пространство. Соответсвенно, в моем мозгу родилась мысль, что это и есть определение
, то мы получим ровно интересующее меня пространство. Соответсвенно, в моем мозгу родилась мысль, что это и есть определение  , но хотелось бы быть уверенной.
, но хотелось бы быть уверенной.
P.S. Производные не классические, а обобщенные.
P.P.S. Непрерывность такой функции я уже получила, так что значок С для пространства оправдан.
Cама статья относится к области мат. физики и нелинейного анализа. Классические учебники (Колмогоров-Фомин, Владимиров и т.д.) ответа на мой вопрос не дали.
В самой статье написано так:
inf - это бесконечность, я не знаю. как ее тут поставить

Короче, суть в том, что если есть функция одной переменной u(t) из
P.S. Производные не классические, а обобщенные.
P.P.S. Непрерывность такой функции я уже получила, так что значок С для пространства оправдан.
Похожие темы
- Ответы
- 26
- Просмотры
- 11K
E
