Приложение
Как установить приложение на iOS
Смотрите видео ниже, чтобы узнать, как установить наш сайт в качестве веб-приложения на домашнем экране.
Примечание: Эта возможность может быть недоступна в некоторых браузерах.
-
Уважаемый посетитель!!!
Если Вы уже являетесь зарегистрированным участником проекта "миХей.ру - дискусcионный клуб",
пожалуйста, восстановите свой пароль самостоятельно, либо свяжитесь с администратором через Телеграм.
Вы используете устаревший браузер. Этот и другие сайты могут отображаться в нём некорректно.
Вам необходимо обновить браузер или попробовать использовать другой.
Вам необходимо обновить браузер или попробовать использовать другой.
Trotil
Команда "У.М."
Freaky написал(а):Должно получиться r= 0,5h??
Это как раз тот корень, который мы должны выкинуть. Правильный второй: h=2/5 r
Кстати, необязательно раскрывать скобки.
a^2 - b^2 = (a-b)(a+b)
R-h/2 = 0 => h = 2R - не подходит
R-5h/2 = 0 => h = 2R/5 - правильный ответ
T
Total
Гость
Помогите пожалуйста решить к среде :
:
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a*(корень из 2) и 2*a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а)меньшую высоту параллелограмма;
б)угол между плоскостью ABC и плоскостью основания;
в)площадь боковой поверхности параллелепипеда;
г)площадь поверхности параллелепипеда.
 :
:1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a*(корень из 2) и 2*a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а)меньшую высоту параллелограмма;
б)угол между плоскостью ABC и плоскостью основания;
в)площадь боковой поверхности параллелепипеда;
г)площадь поверхности параллелепипеда.
B
bulaffka
Гость
Помогите мне,пожалуйста!!!!!!!!Очень срочно надо!!!!!!!!! Хотя бы одну!!!!
1)В конусе через вершину под углом ФИ к плоскости основания проведена плоскость отсекающая от Окр основания дугу в 2Альфа. V - ?
2)Основание прямой призмы - ромб со стороной А и Альфа - острый угол. Секущей плоскать проведена через диагональ основания и противоположную вершину, верх основания составляет с плоскостью основания угла Бета. V - ?
Извините меня за наглость,но мне в среду надо уже сдать! Я уже и не знаю, что делать!
1)В конусе через вершину под углом ФИ к плоскости основания проведена плоскость отсекающая от Окр основания дугу в 2Альфа. V - ?
2)Основание прямой призмы - ромб со стороной А и Альфа - острый угол. Секущей плоскать проведена через диагональ основания и противоположную вершину, верх основания составляет с плоскостью основания угла Бета. V - ?
Извините меня за наглость,но мне в среду надо уже сдать! Я уже и не знаю, что делать!
Sensile
Участник
Total
Зад1
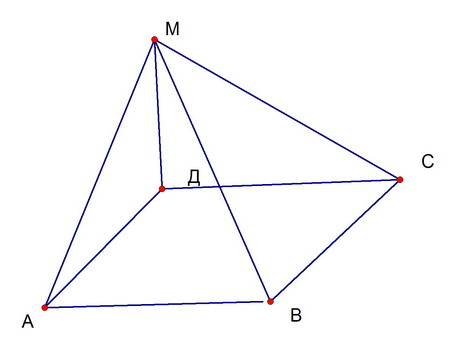
План
1)Треугольники ADM и CDM прямоугольные с катетами а, их площадь стандартно находится.
2)По теореме Пифагора можно найти МА и МС
3)DA пепрендикулярно АВ, DA- проекция МА, поэтому по теореме о трех перпендикулярах МА перпендикулярно АВ, а значит, треугольник МАВ прямоугольный с известными катетами (МА найдено в п. 2, АВ=а), площадь легко находится
4)Аналогично с треугольником МСВ
5) площадь основания - площадь квадрата
6) Складываем найденные площади
Total
Зад2
Известный факт:
Площадь параллелограмма равна произведению сторон на синус угла между ними
Поэтому площадь параллелограмма в основании АВСД равна)sin45=2a^2)
Меньшая высота параллелограмма h - это та? которая опущена на большую сторону
Так пл. параллелограмма равна произведению стороны на высоту, то
S= h*(2a)
отсюда находим h - меньшую высоту параллелограмма и одновременно высоту параллелепипеда
задача а) решена
Зад2 в) и г) теперь решаются элементарно
Боковые ребра перпендикулярны плоскости основания, то есть являются высотами боковых граней и равны найденному h, основания всех боковых граней известны, легко найти площади боковых граней, площадь основания тоже уже найдена
Осталось решить задачу б)
По-видимому в условии опечатка и надо найти угол между плоскостью и плоскостью основания
и плоскостью основания
Построим сначала секущую плоскость
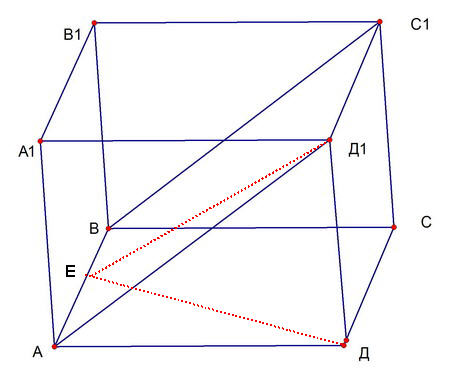
раз она проходит через точки В и , то пересекает грань по прямой
, то пересекает грань по прямой  , а параллельную ей грань по прямой параллельной
, а параллельную ей грань по прямой параллельной  , то есть
, то есть  . Поэтому плоскость
. Поэтому плоскость  дает сечение
дает сечение 
Искомый угол - это угол между плоскостью АВС1Д1 и плоскостью основания
Нам нужно построить линейный угол двугранного угла между этими плоскостями
Линия их пересечения АВ.
Проведем из точки Д перпендикуляр ДЕ к АВ и соединим Е с
Так как перпендикулярно пл. осн., то
перпендикулярно пл. осн., то  наклонная, ДЕ -проекция, по теореме о трех перпендикулярах
наклонная, ДЕ -проекция, по теореме о трех перпендикулярах  тоже перп АВ
тоже перп АВ
Угол - искомый линейный угол. Его надо найти
- искомый линейный угол. Его надо найти
=ДД_1/ДЕ)
 - высота параллелепипеда найдена ранее
- высота параллелепипеда найдена ранее
ДЕ - высота параллелограмма, проведенная в данном случае к меньшей стороне (большая высота)
Как и выше площадь параллелограмма
S= ДЕ*АВ
S, АВ известны, находим ДЕ
И далее тангенс
Зад1

План
1)Треугольники ADM и CDM прямоугольные с катетами а, их площадь стандартно находится.
2)По теореме Пифагора можно найти МА и МС
3)DA пепрендикулярно АВ, DA- проекция МА, поэтому по теореме о трех перпендикулярах МА перпендикулярно АВ, а значит, треугольник МАВ прямоугольный с известными катетами (МА найдено в п. 2, АВ=а), площадь легко находится
4)Аналогично с треугольником МСВ
5) площадь основания - площадь квадрата
6) Складываем найденные площади
Total
Зад2
Известный факт:
Площадь параллелограмма равна произведению сторон на синус угла между ними
Поэтому площадь параллелограмма в основании АВСД равна
Меньшая высота параллелограмма h - это та? которая опущена на большую сторону
Так пл. параллелограмма равна произведению стороны на высоту, то
S= h*(2a)
отсюда находим h - меньшую высоту параллелограмма и одновременно высоту параллелепипеда
задача а) решена
Зад2 в) и г) теперь решаются элементарно
Боковые ребра перпендикулярны плоскости основания, то есть являются высотами боковых граней и равны найденному h, основания всех боковых граней известны, легко найти площади боковых граней, площадь основания тоже уже найдена
Осталось решить задачу б)
По-видимому в условии опечатка и надо найти угол между плоскостью
Построим сначала секущую плоскость

раз она проходит через точки В и
Искомый угол - это угол между плоскостью АВС1Д1 и плоскостью основания
Нам нужно построить линейный угол двугранного угла между этими плоскостями
Линия их пересечения АВ.
Проведем из точки Д перпендикуляр ДЕ к АВ и соединим Е с
Так как
Угол
ДЕ - высота параллелограмма, проведенная в данном случае к меньшей стороне (большая высота)
Как и выше площадь параллелограмма
S= ДЕ*АВ
S, АВ известны, находим ДЕ
И далее тангенс
B
bulaffka
Гость
Trotil, извини,ошиблась немного.Переписываю по-человечески:
1)В конусе через его вершину под углом фи к плоскости основания проведена плоскость,отсекающая от окружности основания дугу 2 альфа. Радиус основания конуса равен R. Найти объем конуса.
2)Основание прямой призмы - ромб со стороной а и Альфа - острый угол. Секущая плоскость проведена через диагональ основания(если смотреть на рисунок Sensile,то диагональ BD) и противоположную вершину, верх основания составляет с плоскостью основания угла Бета. Найти объём призмы.
Надеюсь, что теперь понятно изъяснилась.
1)В конусе через его вершину под углом фи к плоскости основания проведена плоскость,отсекающая от окружности основания дугу 2 альфа. Радиус основания конуса равен R. Найти объем конуса.
2)Основание прямой призмы - ромб со стороной а и Альфа - острый угол. Секущая плоскость проведена через диагональ основания(если смотреть на рисунок Sensile,то диагональ BD) и противоположную вершину, верх основания составляет с плоскостью основания угла Бета. Найти объём призмы.
Надеюсь, что теперь понятно изъяснилась.
B
bulaffka
Гость
Trotil, вы сможете мне помочь?
B
bulaffka
Гость
Через меньшую
Sensile
Участник
bulaffka
Вот чертеж
Угол ВАД равен , поскольку он острый, то ВД меньшая диагональ
, поскольку он острый, то ВД меньшая диагональ
Искомое сечение
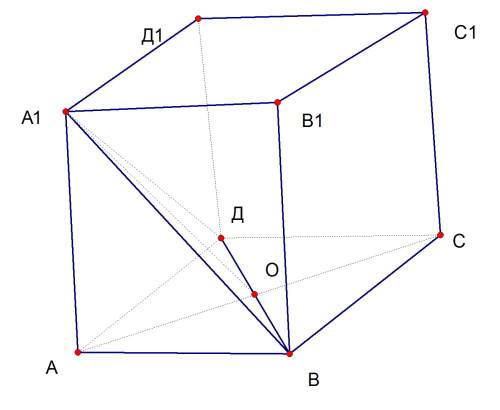
Сейчас напишу решение
Для нахождения объема призмы нужно найти площадь основания и высоту призмы
Площадь любого параллелограмма (в том числе и ромба) можно найти как произведение сторон на синус угла между ними

Далее заметим, что диагонали ромба взаимно перпендикулярны и являются биссектрисами соответствующих углов. Поэтому АО перпендикулярно ВД и угол ДАО= . Рассмотрим треугольник АОД.
. Рассмотрим треугольник АОД. )
Отсюда можно найти АО.
Так как АО перпендикулярно ВД, АО является проекцией , то
, то  тоже перпендикулярно ВД и, следовательно, угол
тоже перпендикулярно ВД и, следовательно, угол  - линейный угол двугранного угла между секущей плоскостью и плоскостью основания
- линейный угол двугранного угла между секущей плоскостью и плоскостью основания
Угол
Рассмотрим треугольник :
: 
Отсюда находим высоту призмы
Объем
Вот чертеж
Угол ВАД равен
Искомое сечение

Сейчас напишу решение
Для нахождения объема призмы нужно найти площадь основания и высоту призмы
Площадь любого параллелограмма (в том числе и ромба) можно найти как произведение сторон на синус угла между ними
Далее заметим, что диагонали ромба взаимно перпендикулярны и являются биссектрисами соответствующих углов. Поэтому АО перпендикулярно ВД и угол ДАО=
Отсюда можно найти АО.
Так как АО перпендикулярно ВД, АО является проекцией
Угол
Рассмотрим треугольник
Отсюда находим высоту призмы
Объем
B
bulaffka
Гость
Спасибо вам огромное!!!!!!!!!
B
bulaffka
Гость
объём конуса равен произведению 1/3 на площадь основания и на высоту
Trotil
Команда "У.М."
B
bulaffka
Гость
Нам не хватает высоты, а прямо сейчас можно посчитать площадь основания - ПR^2